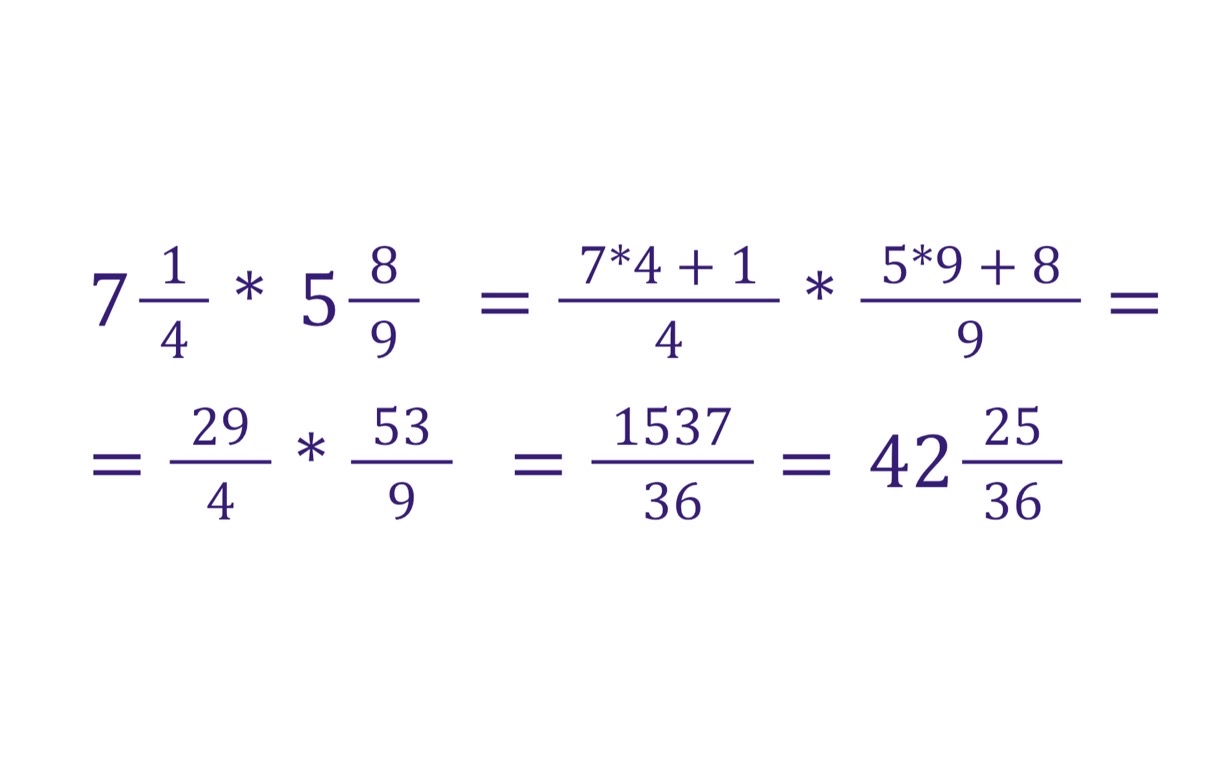Умножение дробей — это одна из наиболее простых операций с дробями, которая требует лишь умножения числителей и знаменателей друг на друга. В отличие от сложения и вычитания, при умножении дробей не нужно приводить их к общему знаменателю. В этой статье мы рассмотрим основные правила умножения дробей, сократим результат и разберем примеры с участием смешанных дробей.
Основные правила умножения дробей
Для умножения дробей достаточно умножить числители дробей друг на друга и знаменатели друг на друга. После выполнения умножения результат может быть упрощен, если числитель и знаменатель имеют общие делители.
Пример:
Умножим 2/3 и 4/5.
- Умножаем числители:
- 2 * 4 = 8.
- Умножаем знаменатели:
- 3 * 5 = 15.
- Получаем дробь:
- 8/15.
Таким образом, 2/3 * 4/5 = 8/15.
Сокращение дробей после умножения
После умножения дробей иногда можно сократить результат. Для этого нужно найти общий делитель числителя и знаменателя и разделить оба на это число.
Пример:
Умножим 6/8 на 4/9.
- Умножаем числители:
- 6 * 4 = 24.
- Умножаем знаменатели:
- 8 * 9 = 72.
- Получаем дробь:
- 24/72.
- Сократим дробь на 24:
- 24/72 = 1/3.
Таким образом, 6/8 * 4/9 = 1/3.
Умножение смешанных дробей
Перед умножением смешанных дробей их нужно преобразовать в неправильные дроби, затем умножить их, как обычные дроби.
Пример:
Умножим 1 1/2 на 2 2/3.
- Преобразуем смешанные дроби в неправильные:
- 1 1/2 = 3/2.
- 2 2/3 = 8/3.
- Умножаем дроби:
- (3/2) * (8/3) = 24/6 = 4.
Таким образом, 1 1/2 * 2 2/3 = 4.
Умножение дроби на целое число
Когда дробь умножается на целое число, числитель дроби умножается на это число, а знаменатель остается неизменным.
Пример:
Умножим 5/8 на 3.
- Умножаем числитель дроби на целое число:
- 5 * 3 = 15.
- Оставляем знаменатель без изменений:
- 15/8.
- Преобразуем результат в смешанную дробь:
- 15/8 = 1 7/8.
Таким образом, 5/8 * 3 = 1 7/8.
Заключение
Умножение дробей — это одна из самых простых операций с дробными числами, которая требует лишь базовых навыков арифметики. Сокращение дробей после умножения помогает упростить результат и делает его более удобным для использования. Освоив умножение дробей, вы сможете легко решать задачи с дробями в математике и в повседневной жизни.